一类双曲辛映射的规范型毕业论文
2020-07-08 21:48:14
摘 要
本文用KAM的方法讨论了哈密顿系统的离散形式--辛映射的规范型,因为辛映射没有固定的规范型,因此在处理由KAM迭代所产生的小分母问题时会有一定的难度,本文的研究的对象是一类双曲的辛映射。
关键词:辛映射,KAM理论,同调方程,小分母问题
Abstract
This article use the method of notes form of discrete Hamiltonian system was discussed, mapping the specification of the type, because there is no fixed type specification of symplectic map, so in dealing with small produced by notes iteration the denominator will have certain difficulty, this article research object is a kind of hyperbolic symplectic map.
Key words: symplectic mapping, KAM theory, homology equation, small denominator problem
目录
一 、引言和基本概念 |
1.1 哈密顿系统……………………………………………………………4
1.2 辛矩阵…………………………………………………………………4
1.3 辛同胚…………………………………………………………………5
1.4 生成函数………………………………………………………………5
1.5 KAM 理论………………………………………………………………6
二、 主要结果的证明 |
2.1 小分母问题的产生背景………………………………………………7
2.2 高维下的小分母问题…………………………………………………8
2.3低维双曲线的小分母问题……………………………………………11
2.4 测度估计………………………………………………………………21
三、 参考文献 | 22 |
- 引言和基本概念
1.1哈密顿系统
形如下列含有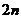 个方程的一阶常微分方程组叫做哈密顿系统。
个方程的一阶常微分方程组叫做哈密顿系统。
具体形式如下:
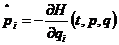 ,
,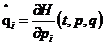 ,
,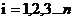
其中,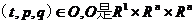 上的开区域,
上的开区域,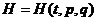 是O上的光滑函数,常称为哈密顿函数,其中向量
是O上的光滑函数,常称为哈密顿函数,其中向量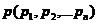 ,
,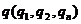 为一对共轭向量。
为一对共轭向量。 为时间变量。为了方便讨论,引进
为时间变量。为了方便讨论,引进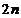 维列向量
维列向量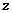 和
和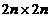 反对称矩阵
反对称矩阵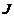 以及梯度
以及梯度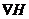
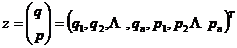 (1.1)
(1.1)
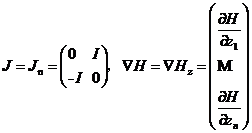 ,
,
其中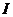 是
是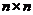 单位阵,此时(1.1)可以表示为
单位阵,此时(1.1)可以表示为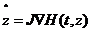 。
。
1.2辛矩阵
一个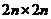 矩阵
矩阵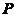 有:
有:
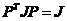 ,
,
那么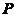 就是一个辛矩阵
就是一个辛矩阵
对于
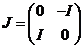
 是
是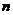 阶单位矩阵并且是一个单位矩阵
阶单位矩阵并且是一个单位矩阵
另外,如果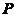 同时满足
同时满足
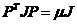 ,
,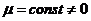 ,
,
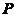 是以
是以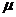 为辛矩阵,这里
为辛矩阵,这里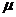 是乘子。
是乘子。
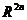 记为
记为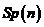 ,因为它是一个典型的类(Lie)群。
,因为它是一个典型的类(Lie)群。
课题毕业论文、开题报告、任务书、外文翻译、程序设计、图纸设计等资料可联系客服协助查找。



